Modern man lives isolated in his artificial environment, not because the artificial is evil as such, but because of his lack of comprehension of the forces which make it work—of the principles which relate his gadgets to the forces of nature, to the universal order. It is not central heating which makes his existence “unnatural,” but his refusal to take an interest in the principles behind it. By being entirely dependent on science, yet closing his mind to it, he leads the life of an urban barbarian.
— Arthur Koestler (1969). “The Act of Creation”
A willingness to learn and understand how the world around you works is important, not only because of the personal benefit you gain, but also because it is a sign of respect to those whose ideas and effort built the world around us. I don't mean to say we should strive for complete understanding of every technology that we use in our daily lives, as this is impossible. However, it is not an understatement to say that our modern existence is largely a result of the work of a handful of great minds. I find it enriching to gain some level of understanding behind the ingenious ideas that have propelled us to these great heights of prosperity.
If nothing else, I think the men and women behind these ideas would be grateful that those who benefit from them make the effort to understand their inception. As humans we all want to be remembered and recognized for the impact we've had on the world around us. However, I think it is also common for those responsible for such important accomplishments to yearn for more than just recognition. Fame, wealth, awards and prestige are all fair to expect if you are the individual behind an important breakthrough or invention. This is what makes Claude Shannon's indifference to all those aspects that come with the territory of being such an accomplished scientist so interesting. He had no desire for the spotlight, because he did not solve the problems he did for recognition; he simply was a curious mind that wanted to understand and formulate the underlying patterns of the world around him.

A Mind At Play is a biography of Claude Shannon's life. It was authored by two individuals, Jimmy Soni and Rob Goodman - both of whom have no formal technical background. They were inspired to write the book after learning about Shannon from a friend, and they found it intriguing someone considered one of the founding fathers of today's digital age, and the inventor of the most important theory in communications is largely unknown to the general public. Although his impact is arguably comparable to the likes of Einstein, Tesla, and Von Neumann, he is normally not included in this scientific pantheon. I myself had not heard of him before hearing of this book, so it goes without saying that I was certainly interested after hearing of his accomplishments. As the title suggests, Shannon is most known for ushering in the era of digital communication due to his groundbreaking thesis, A Mathematical Theory of Communication. His theory, commonly referred to as Information Theory, completely revolutionized how scientists and engineers viewed communication.
Claude Shannon's paper accomplished two important things that would eventually revolutionize communications. Firstly, he formalized an abstraction which can be used to describe ANY type of communications medium. And secondly, Shannon devised an ingenious schema (with proofs to support it) that allows for ANY message to be sent without error, no matter how noisy the transmission channel is.
His first accomplishment provided the ability to talk about any transmission medium using the same language. This includes telegraphy, telephony, TV, radio, human speech, and anything which involves the transfer of information from a source to receiver. The features that Shannon decided are the integral components of communication are illustrated in the block diagram below, taken from his original paper:
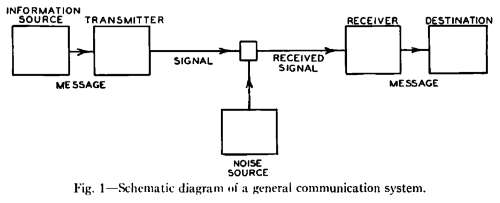
These components would serve as the base from which Shannon would introduce his new theory of information, and would also become the standard vernacular for all communications in the years to come.
As part of this abstraction, Shannon needed to rigorously define what was meant by "information", and how to quantify it. This actually proved to be one of his most astounding leaps in ingenuity, because before him it was assumed that the amount of information in a message is tied to the meaning of the message. Shannon showed that it is only based off the encoding with which you use to send it; it is simply the content of the message which determines the amount of information it contained, not how the receiver is to interpret it. This may sound quite obvious to our modern ears, but you should understand that our abundance of information technologies, and their agnostic nature to the type of information they manipulate, has shaped our intuitions much differently than in Claude Shannon's era. In his own words, information is the "resolution of uncertainty".
In other words, sending a letter from a set of 26 possible letters is objectively more information than sending a binary digit (choosing from only 0 or 1). Furthermore, in the context of transmitting English writing, the sending of the letter "Q" provides more information to the receiver in contrast with sending an "S". This is because Q is much less likely to appear in English text than S, so a Q tells the receiver more. To illustrate this better, imagine receiving the following message from someone :
I hid the keys underneath the [S|Q]...
where the final letter is either an S or a Q. If for some reason the end of the message was cut off before you could receive the rest, your chances of finding the hidden keys would be much different depending on what that final letter received was. Since there are far more words which start with the letter S than with the letter Q1, you would actually have received more information if the final letter was a Q. I can think of only a handful of things you may find in a house which begin with a Q (Quilt, Qur'an, Quiche), but I definitely would not want to begin checking underneath everything in my house that begins with an S for the keys.
Similarly, say the letter was a Q but you actually received one more letter of the word after that - would you be able to guess what it is? Of course you would because nearly every occurrence of the letter Q in the English language is followed by a "U". Because of its predictability, it is also fair to say that the "U" carries very little information with it. These patterns of redundancy in English are very common, so much so that Shannon once estimated that as much as 80% of all English text on earth could be stripped away without us losing any information! As I will explain shortly however, in the communications realm this redundancy serves an important purpose.
With the basic components of communication as well as a new, more useful definition of information at his disposal, Claude Shannon could now solve two important problems that has plagued the transmission of information up until then. The first was, how do you transmit information through a limited bandwidth channel in the most efficient way possible. The advantage of knowing such a solution I believe are quite obvious, especially for Shannon's employer at the time and the owner of the largest telephone infrastructure network in America, Bell. The second problem he solved was how can you ensure a message will be received accurately over a noisy channel, essentially limiting the rate of error to be as arbitrarily low as desired. This was an enormous achievement in the field of communications, providing accuracy to noisy channels such as Trans-Atlantic undersea cables which had not had much success up until that point, or even the millions of kilometres of open space which separate Earth and a voyaging spacecraft.
As it turns out, you can't have your cake and eat it too. Or more directly, you can't have perfectly efficient information transfer without (the risk of) errors too. As it is with most technologies, desirable qualities usually come at a trade-off. It is not a mutually exclusive trade-off however, as a transmission encoding can still utilize Shannon's theorems and see gains in both efficiency (or "speed") and accuracy.
I won't get into the technical details in this review, mostly because I don't know them, and I'm also on a subway right now so I can't look them up. But I'll explain what I understand of these ideas from a high-level.
To achieve the most efficient transfer of information possible, you must first understand the domain of information that you want to transfer, and how you want to represent that information in a finite set of symbols. You must then determine how often the symbols appear on average, which is the tricky part as information transfer is a stochastic process, which means it is partly random and partly deterministic. The better you can predict these frequencies, the better your encoding scheme will be.
For example, if you want to develop an encoding for English text, your set of symbols would consist of the alphabet, plus maybe digits and punctuation too. The next question you ask is how do I transform these symbols into units of information (most likely sequences of bits) for transfer over a physical channel. Well you may start with letter frequencies and determine that you should use the least amount of bits to represent an "E" and more bits to represent rarer letters like "Q". This will guarantee better transmission rates. The exact procedure for making these codes was first proposed by Shannon in his paper, and later improved by Robert Fano and then David Huffman.
The hard part is optimizing your encoding scheme, because as you optimize it more and more you begin a trade-off with error likelihood. As an example, suppose you notice that even certain words appear far more often than the rare letters, like "the" or "to" - so you may consider assigning them shorter bit sequences than those rare letters, essentially expanding your set of symbols which you use to represent the information. What could be wrong with that?
Well, nothing is wrong with that technically. If you extend this idea further, there is essentially nothing wrong with using single symbols to represent entire sentences and paragraphs! If you can identify these common patterns and assign them unique encodings which are shorter than their corresponding encodings would have been with our original letter symbols, you will certainly become more efficient.
The problem arises when you consider that encodings composed of discrete sequences of information units (think "bits"), and there is only a finite domain of possible permutations of these units. So as you begin to utilize this domain more the symbol encodings begin to back onto one another, or rather they become quite similar to each other perhaps only differing by a single bit. At this point your über efficient encoding scheme is now vulnerable to errors!
Every physical transmission channel is subject to some amount of noise. If you are in a loud room speaking right beside a friend, your conversation is still (literally) subject to noise and the chance of a misunderstanding is definitely non-zero. Some channels are inherently noisier than others, but what is a tolerable error rate is based on the application and context. How do you reduce it though? The answer is you get rid of those silly encodings for entire sentences and you instead move in the opposite direction, you add bits to your encodings!
Figuring out what sort of encodings reduce error is where mathematical rigor is really going to help the most. As far as I know, there are two main strategies, the first being simple redundancy. Repeating yourself will inherently protect your information from failing due to single transient errors, and that shouldn't be too hard to grasp. The second strategy involves how you actually design your encoding scheme and how much "distance" you have between different codes. Some really smart people took Shannon's ideas and formalized this strategy, in particular another Bell Labs alumnus, Richard Hamming, invented a generalized family of linear-error detecting and correcting codes called Hamming codes. These sorts of codes can be "resistant" to a certain amount of error; they can be single-error tolerant, double-error tolerant etc.
And that's basically it - as far as my understanding of Shannon's information theory goes. I think the really important consequence of Shannon's thesis was that he showed everything can be digitized, every communication, every type of information. This was a groundbreaking revolution in what was still largely an analog world at that time. He laid the first stone in what would eventually become the vast digital landscape we find ourselves in today.
How about the book? I normally write about the book but I think I've mostly tried to explain information theory so far, which I'm hoping turned out somewhat coherent. Anyways, I found A Mind At Play to be a pretty interesting read. I think that's largely in part due to my interest in the subject as well as the type of person Claude Shannon was. I enjoy reading about extraordinary individuals and their personalities. I found a lot to admire about Shannon, especially his indifference to fame and wealth. By all accounts it seems like Shannon was driven by his curiosity in how things work; he couldn't live with a problem and not knowing the solution. That's the sort of motivation I aspire to attain and maintain throughout life. Shannon's other defining characteristic was his playful nature and his fascination with toys and games. What was remarkable was when these two qualities intersected. Shannon would do things like write papers and build machines to explore the games he was interested in. I actually decided to build a chess engine after reading his 1965 paper about how one would go about programming one, long before it was possible to do so. His explanation seemed so clear and simple that I decided to give it a try.
The book itself wasn't the greatest non-fiction I've ever read, nor even the best biography I've ever read. I enjoyed Steve Jobs biography more, I think it did a better job of exploring his character. A Mind At Play felt a little too encyclopedic at times, maybe spending too much time on details that don't tell you anything new about Claude Shannon. This might be because it is a postmortem biography, and most of Shannon's life occurred half a century ago. Overall though, the book kept me entertained and engaged throughout its entirety. If you are interested in technology at all I'd definitely recommend it.
In keeping with tradition for my non-fiction reviews, I'll highlight a few of my favourite quotes.
highlight 1
From the God’s-eye view, there is a law of tides; from our earthbound view, only some petty local ordinances.
— Jimmy Soni, "A Mind at Play" pg. 49
Nice way of expressing the idea of perfect information and the deterministic nature of the universe. I think of the complexity of forces and interactions which govern the movement of the oceans, and how it would be impossible to model it perfectly, yet we see the microscopic results of these enormous forces in every wave and small ripple that rolls towards shore. The "law of tides" are the aggregate effects of every law of physics acting on the particles of water at all times, something we can know in totality, yet something we can approximate with our "local ordinances". Our laws cannot predict the motion of each wave rolling in to every beach on earth, yet their existence is proof of their obedience to all these forces acting upon them.
highlight 2
At the same time, Bush’s influence in the engineering world won Shannon’s thesis the unfortunately named Alfred Noble Prize (unfortunately named, because this is the point at which every writer mentioning it points out that it has no relation to Alfred Nobel’s much more famous prize).
— Soni, pg. 88
highlight 3
"I’m a machine and you’re a machine, and we both think, don’t we?"
— Claude Shannon, pg. 337
Asked in 1989 whether he thought machines could "think," Shannon replied with the question above. Shannon's stance towards artificial intelligence seemed to shift throughout the years, from optimism to a sort of indifferent misanthropic view. He stated that if machines were meant to take over control of humanity, then they should, and he even listed some of a machines better nature's which would make them better leaders than us. Besides this slightly depressing take on the future of AI, it is still interesting to note that one of the founding fathers of our digital age was very certain of not just the possibility, but also the eventuality of the existence of thinking machines. He held this mindset over half a century ago no less.
highlight 4
Years earlier, Shannon had set his mind to the question of this funeral—and imagined something very different. For him, it was an occasion that called for humor, not grief. In a rough sketch, he outlined a grand procession, a Macy’s–style parade to amuse and delight, and to sum up the life of Claude Shannon. The clarinetist Pete Fountain would lead the way, jazz combo in tow. Next in line: six unicycling pallbearers, somehow balancing Shannon’s coffin (labeled in the sketch as “6 unicyclists/1 loved one”). Behind them would come the “Grieving Widow,” then a juggling octet and a “juggling octopedal machine.” Next would be three black chess pieces bearing $100 bills and “3 rich men from the West”—California tech investors—following the money. They would march in front of a “Chess Float,” atop which British chess master David Levy would square off in a live match against a computer. Scientists and mathematicians, “4 cats trained by Skinner methods,” the “mouse group,” a phalanx of joggers, and a 417-instrument band would bring up the rear.
This proved impractical. And his family, understandably, preferred a tamer memorial. Shannon was laid to rest in Cambridge, along the Begonia Path in Mount Auburn Cemetery.— Soni, pg. 455
Reading about Shannon's wishes for his funeral procession shows the type of he was, in a weird ironic way. Shannon was consistently averse to any sort of extravagence and celebrity when it came to him and his work. Shannon had no desire for fame and adulation from anyone for what he accomplished, even though he most certainly deserved it. Which is why it is hilarious to me that he desired the most over-the-top pompous circus of performances to accompany funeral procession. His written explanation was that he wanted the occasion to call for "humour", not grief, and that essentially he just wanted everyone to have a good time. I think this is probably partially true, but I also think Shannon had a dark humour, and deep-down he understood the needless overtures and traditions we use to remove ourselves from our mortality, but that this is also very much an expression of our human nature. We shy away from death and treat funerals with such delicacy that I think Shannon sought to "break the ice" with regards to his own funeral anyways with a loud, colourful display of outrageous proportions.
1http://funbutlearn.com/2012/06/which-english-letter-has-maximum-words.html